베이즈에 의하면 Classification 문제에서 다음과 같은 확률모델에 기반한 Classifier가 Error를 최소화한다는 것을 보장한다. (참고: http://arkainoh.blogspot.kr/2017/09/bayesian.decision.theory.html)
문제는 이 우변의 확률을 구하는 방법이다. 물론 베이즈 정리(Bayes’ Theorem)를 통해 Posterior Probability를 간단히 구할 수 있다.
하지만, 오른쪽 변에 있는 Likelihood, Prior Probability 등의 확률이 주어지지 않은 경우에는 Posterior Probability를 구할 수 없다.
따라서, Parametric Learning에서는 이렇게 구하고자 하는 확률들이 일종의 함수라고 가정하고, 그 함수의 Parameter들을 데이터 기반의 학습을 통해 특정하는 식으로 접근한다. 이는 쉽게 말해서, 기계학습에서 h(x) = ax + b라는 함수를 구하고자 할 때, 함수의 형태는 직선인 것을 알고 있지만 a와 b라는 Parameter를 모르는 상황과 유사하다. 이때 다양한 학습 기법을 통해 a와 b의 값을 특정하게 된다.
따라서, Parametric Learning에서는 이렇게 구하고자 하는 확률들이 일종의 함수라고 가정하고, 그 함수의 Parameter들을 데이터 기반의 학습을 통해 특정하는 식으로 접근한다. 이는 쉽게 말해서, 기계학습에서 h(x) = ax + b라는 함수를 구하고자 할 때, 함수의 형태는 직선인 것을 알고 있지만 a와 b라는 Parameter를 모르는 상황과 유사하다. 이때 다양한 학습 기법을 통해 a와 b의 값을 특정하게 된다.
다시 말해서, 함수의 형태는 주어진다고 가정하고 학습 데이터를 바탕으로 함수의 Parameter들을 학습하는 것이 바로 Parametric Method의 접근 방식이다. 이 글에서는 Parametric Learning의 가장 대표적인 방법 중 하나인 최대 가능도 추정(Maximum Likelihood Estimation)에 대해 살펴보도록 하겠다.
2. Maximum Likelihood Estimation (MLE)
Parameter는 함수의 세부적인 형태를 결정하는 요소다. 대표적인 예로, 정규분포(Normal Distribution)의 Parameter는 각 데이터 샘플들의 평균과 분산이라고 할 수 있다. 평균은 정규분포 그래프의 수평 위치를 결정하고, 분산은 폭을 결정한다.
실제로, 현실 세계에서 확률 분포를 따르는 다양한 사건들은 정규분포를 따르는 경우가 많다. 그렇다면, 정규분포의 형태를 갖는 함수를 학습하는 두 가지 예제를 통해 Parametric Learning의 학습 방법에 대해 알아보도록 하자.
데이터는 동전이 앞면인 경우 1, 그리고 뒷면인 경우를 0으로 하여 D = [1 0 1 1]과 같은 벡터로 주어진다. 동전 던지기의 경우는 베르누이 분포(Bernoulli Distribution)를 따르기 때문에, 0 또는 1의 값을 가지는 확률 변수 x에 대해 P(x = 1) = θ이고, P(x = 0) = 1 - θ이 된다. 이 두 가지를 합쳐서 P(x)를 정의하면 다음과 같다.
그리고 동전을 던지는 각각의 시행은 서로 독립적(Independent)이기 때문에 주어지는 D의 전체 확률은 각 시행의 확률을 모두 곱하면 구할 수 있다. 따라서, 동전의 종류에 따라 θ의 값이 다를 것이기 때문에 임의의 동전을 네 번 던질 경우 다음과 같은 확률들이 나올 수 있다.
n 번째 시행에서의 x값을 xⁿ이라고 정의할 경우 Likelihood는 다음과 같이 구할 수 있다.
함수 f(x)의 최댓값 또는 최솟값을 반환하는 해 x를 구하는 문제에서는 로그(Log)를 취해도 그 결과가 같기 때문에, 계산 편의를 위해 Likelihood에 Log를 취하도록 한다. Log를 취한 뒤 θ에 대해 미분을 한 값을 0이라고 놓고 풀면 P(D|θ)가 최대가 될 때의 θ를 구할 수 있다.
(2) Multinomial Distribution
앞선 동전 던지기는 Bernoulli Distribution을 따르는 경우였다. 하지만 딥 러닝과 같이 기계학습에 기반한 대부분의 Classification 문제들은 2개 이상의 많은 Class로 데이터들을 분류해야 한다. 즉, 확률변수 x가 다항 분포(Multinomial Distribution)를 따르는 경우이다.
확률변수 x가 가질 수 있는 특정 값을 v라고 하면, Class가 총 k개 있다고 가정할 경우 x는 {v1, v2, v3, ..., vk} 중 한 개의 값을 갖게 된다.
x가 vi의 값을 가질 확률을 θi라고 하면 다음과 같이 정리할 수 있다.
동전 던지기 예제와 마찬가지로 Likelihood에 Log를 씌워서 최댓값이 될 때의 θ를 구하도록 하자.
그런데, 여기서 주의할 점이 하나 있다. 앞선 Bernoulli Distribution 예제에서는 이 값을 θ에 대해 미분한 뒤 0으로 놓고 풀었지만, 이 경우에는 오류가 발생할 수 있다.
앞서 정리 했듯이 각각의 Class에 해당하는 θ들의 합은 1이라는 조건을 만족해야 한다. 그런데 만약 단순히 미분을 한 뒤 극대, 극소를 찾게 되면 이 조건을 위반할 가능성이 있다. 따라서 이러한 문제를 해결하기 위해서는 다른 방법을 적용해야 한다. 특정 조건을 만족하면서 최댓값 또는 최솟값을 구하는 문제에서는 라그랑주 승수법(Lagrange Multiplier Method)을 사용한다. (참고: http://arkainoh.blogspot.kr/2017/10/lagrange.multiplier.method.html)
임의의 상수 λ를 사용하여 L = f(θ) - λg(θ) 형식으로 놓고 ∇L = 0일 때의 λ와 θ를 구하면 된다. 이때, f(θ)는 최댓값 또는 최솟값을 구하고자 하는 대상 함수이고, g(θ)는 만족해야 할 조건이다. g(θ) = 0이 되도록 식을 정리한 뒤 대입하면 된다.
결과적으로 θi는 주어진 학습 데이터에서 x = vi인 경우의 수를 전체 데이터 샘플의 수(N)로 나누어준 것이다. 이것도 역시 당연한 결과라고 할 수 있다. 1, 2, 3 중 하나의 값을 가질 수 있는 확률 변수 x가 있고 학습 데이터가 D = [1 2 2 2 3 3 2 2]로 주어진다면, P(x = 2) = 5 / 8이라고 간단하게 생각할 수 있는 것이다.
이렇게 당연하다고 생각했던 결과들이 Maximum Likelihood Estimation을 통해 증명된다. 그런데, 이 MLE 방식은 만약 동전을 n 번 던졌을 때 n 번 모두 앞면이 나오는 극단적인 경우에는 해당 동전이 앞면만 나오는 동전이라는 결론을 내려버린다. 이러한 문제를 보완하기 위해 최대 사후 확률 추정(Maximum a Posteriori Estimation), 줄여서 MAP라는 방식을 사용하기도 한다. MAP에 대해서는 다른 글에서 다루도록 하겠다.
Parameter는 함수의 세부적인 형태를 결정하는 요소다. 대표적인 예로, 정규분포(Normal Distribution)의 Parameter는 각 데이터 샘플들의 평균과 분산이라고 할 수 있다. 평균은 정규분포 그래프의 수평 위치를 결정하고, 분산은 폭을 결정한다.
실제로, 현실 세계에서 확률 분포를 따르는 다양한 사건들은 정규분포를 따르는 경우가 많다. 그렇다면, 정규분포의 형태를 갖는 함수를 학습하는 두 가지 예제를 통해 Parametric Learning의 학습 방법에 대해 알아보도록 하자.
(1) Bernoulli Distribution: 동전 던지기
통상적으로 동전을 던졌을 때 앞면 혹은 뒷면이 나올 확률은 0.5라고 생각한다. 하지만, 정말 앞면 혹은 뒷면이 나올 확률이 정확히 반반일까? 답은 No다. 0.5라는 수치는 다른 모든 변수들을 고려하지 않고 동전의 앞, 뒷면이 완벽히 대칭적으로 만들어졌다는 가정에서 나온 것이다. 사실 현실에서는 동전을 던질 때의 힘이나 각도, 그리고 동전 자체의 구성 성분 및 모양 등 다양한 변수가 작용하기 때문에 0.5라는 정확한 확률이 나오지 않을 수도 있다. 따라서 동전의 앞면 혹은 뒷면이 나올 확률 자체를 Parameter라고 보고, 이를 데이터를 통해 경험적으로 학습하고자 한다.
동전의 앞면이 나오는 경우를 h, 뒷면이 나오는 경우를 t라고 할 때, 네 번의 동전 던지기를 시행했더니 h, t, h, h의 순서로 결과가 나왔다고 하자. 이를 학습 데이터로 하여 동전의 앞면이 나올 확률 θ(Theta)를 구하고자 한다. Parameter라는 것을 표기할 때는 상투적으로 θ를 사용한다.통상적으로 동전을 던졌을 때 앞면 혹은 뒷면이 나올 확률은 0.5라고 생각한다. 하지만, 정말 앞면 혹은 뒷면이 나올 확률이 정확히 반반일까? 답은 No다. 0.5라는 수치는 다른 모든 변수들을 고려하지 않고 동전의 앞, 뒷면이 완벽히 대칭적으로 만들어졌다는 가정에서 나온 것이다. 사실 현실에서는 동전을 던질 때의 힘이나 각도, 그리고 동전 자체의 구성 성분 및 모양 등 다양한 변수가 작용하기 때문에 0.5라는 정확한 확률이 나오지 않을 수도 있다. 따라서 동전의 앞면 혹은 뒷면이 나올 확률 자체를 Parameter라고 보고, 이를 데이터를 통해 경험적으로 학습하고자 한다.
데이터는 동전이 앞면인 경우 1, 그리고 뒷면인 경우를 0으로 하여 D = [1 0 1 1]과 같은 벡터로 주어진다. 동전 던지기의 경우는 베르누이 분포(Bernoulli Distribution)를 따르기 때문에, 0 또는 1의 값을 가지는 확률 변수 x에 대해 P(x = 1) = θ이고, P(x = 0) = 1 - θ이 된다. 이 두 가지를 합쳐서 P(x)를 정의하면 다음과 같다.
그리고 동전을 던지는 각각의 시행은 서로 독립적(Independent)이기 때문에 주어지는 D의 전체 확률은 각 시행의 확률을 모두 곱하면 구할 수 있다. 따라서, 동전의 종류에 따라 θ의 값이 다를 것이기 때문에 임의의 동전을 네 번 던질 경우 다음과 같은 확률들이 나올 수 있다.
0.5⁴Parametric Learning에서는 이러한 확률들 중에서 가장 D가 나올 확률이 높은 경우를 찾는 것을 목표로 한다. 즉, P(D|θ)가 최대가 되는 θ를 찾는 것이다. 이때 P(D|θ)는 Likelihood라고 부르기 때문에, 이러한 접근 방법을 Maximum Likelihood Estimation(MLE)라고 한다.
0.9³ * 0.1
0.1³ * 0.9
...
n 번째 시행에서의 x값을 xⁿ이라고 정의할 경우 Likelihood는 다음과 같이 구할 수 있다.
함수 f(x)의 최댓값 또는 최솟값을 반환하는 해 x를 구하는 문제에서는 로그(Log)를 취해도 그 결과가 같기 때문에, 계산 편의를 위해 Likelihood에 Log를 취하도록 한다. Log를 취한 뒤 θ에 대해 미분을 한 값을 0이라고 놓고 풀면 P(D|θ)가 최대가 될 때의 θ를 구할 수 있다.
D = [1 0 1 1]인 경우 이 과정을 통해 θ = 3 / 4라는 결과를 얻게 된다. 어떻게 보면 당연한 결과다. 특정 동전을 네 번 던졌을 때 앞면이 세 번, 뒷면이 한 번 나왔으므로 해당 동전의 앞면이 나올 확률은 3 / 4이다. 이렇게 당연하다고 생각했던 것이 사실은 Maximum Likelihood Estimation의 결과였던 것이다.
(2) Multinomial Distribution
앞선 동전 던지기는 Bernoulli Distribution을 따르는 경우였다. 하지만 딥 러닝과 같이 기계학습에 기반한 대부분의 Classification 문제들은 2개 이상의 많은 Class로 데이터들을 분류해야 한다. 즉, 확률변수 x가 다항 분포(Multinomial Distribution)를 따르는 경우이다.
확률변수 x가 가질 수 있는 특정 값을 v라고 하면, Class가 총 k개 있다고 가정할 경우 x는 {v1, v2, v3, ..., vk} 중 한 개의 값을 갖게 된다.
x가 vi의 값을 가질 확률을 θi라고 하면 다음과 같이 정리할 수 있다.
동전 던지기 예제와 마찬가지로 Likelihood에 Log를 씌워서 최댓값이 될 때의 θ를 구하도록 하자.
그런데, 여기서 주의할 점이 하나 있다. 앞선 Bernoulli Distribution 예제에서는 이 값을 θ에 대해 미분한 뒤 0으로 놓고 풀었지만, 이 경우에는 오류가 발생할 수 있다.
앞서 정리 했듯이 각각의 Class에 해당하는 θ들의 합은 1이라는 조건을 만족해야 한다. 그런데 만약 단순히 미분을 한 뒤 극대, 극소를 찾게 되면 이 조건을 위반할 가능성이 있다. 따라서 이러한 문제를 해결하기 위해서는 다른 방법을 적용해야 한다. 특정 조건을 만족하면서 최댓값 또는 최솟값을 구하는 문제에서는 라그랑주 승수법(Lagrange Multiplier Method)을 사용한다. (참고: http://arkainoh.blogspot.kr/2017/10/lagrange.multiplier.method.html)
임의의 상수 λ를 사용하여 L = f(θ) - λg(θ) 형식으로 놓고 ∇L = 0일 때의 λ와 θ를 구하면 된다. 이때, f(θ)는 최댓값 또는 최솟값을 구하고자 하는 대상 함수이고, g(θ)는 만족해야 할 조건이다. g(θ) = 0이 되도록 식을 정리한 뒤 대입하면 된다.
결과적으로 θi는 주어진 학습 데이터에서 x = vi인 경우의 수를 전체 데이터 샘플의 수(N)로 나누어준 것이다. 이것도 역시 당연한 결과라고 할 수 있다. 1, 2, 3 중 하나의 값을 가질 수 있는 확률 변수 x가 있고 학습 데이터가 D = [1 2 2 2 3 3 2 2]로 주어진다면, P(x = 2) = 5 / 8이라고 간단하게 생각할 수 있는 것이다.
이렇게 당연하다고 생각했던 결과들이 Maximum Likelihood Estimation을 통해 증명된다. 그런데, 이 MLE 방식은 만약 동전을 n 번 던졌을 때 n 번 모두 앞면이 나오는 극단적인 경우에는 해당 동전이 앞면만 나오는 동전이라는 결론을 내려버린다. 이러한 문제를 보완하기 위해 최대 사후 확률 추정(Maximum a Posteriori Estimation), 줄여서 MAP라는 방식을 사용하기도 한다. MAP에 대해서는 다른 글에서 다루도록 하겠다.
3. References
Alpaydın, Ethem. Introduction to machine learning. Cambridge, MA: MIT Press, 2014. Print.









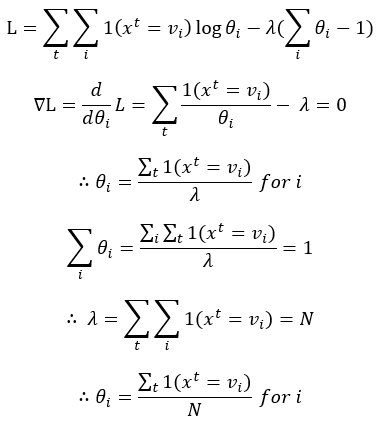
![[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIsNbQ5x9v-Z-WFogOWc-Lns6r9bJLAy9DBCVnl33dXsyXViNgjXrSvmnXzfOeL8m5Wb5VqImEKI0L-B9ZXzc2XmgWpmKCVFv87svXDsHG5WO_4sqVg-y2sRtuqbStxGf2HQ28wBdKIKBV/w72-h72-p-k-no-nu/%25EA%25B3%25A0%25EC%25A0%2595+%25EC%2586%258C%25EC%2588%2598%25EC%25A0%2590+%25EA%25B7%25B8%25EB%25A6%25BC.PNG)


![[R] 다중 회귀 분석 (Multiple Regression Analysis)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcv_-dAHO3EpXA84aAoidUMHJU6rKRsfYflGImKb829FBTDDyw01WftJ-PZD_UakTKM4u5KeubMIaau5zkwBtuYXPqdkpbvFOI_Tv3FFjKFYxkCaKknGFyclAUQrJlzyGwOtLzvotXhTFT/w72-h72-p-k-no-nu/%25ED%259A%258C%25EA%25B7%2580+%25EB%25B6%2584%25EC%2584%259D.PNG)

댓글 없음:
댓글 쓰기