기계학습(Machine Learning)의 가장 핵심적인 목표는 인간이
알지 못하는 함수를 발견하는 것이다. 예를 들어, 날씨를
예측하기 위한 함수를 만든다면 y = C(x)로 표현할 수 있다. 이때 x는 구름의 양 혹은 바람의 세기 등 다양한 변수가 될 것이고, y는
예측된 날씨를 나타내며, C라는 함수는 다양한 변수를 Input으로
받아서 날씨를 Output으로 내놓는 역할을 하게 될 것이다. 이때
이 C는 Target Concept, 즉, 우리가 알고자 하는 세상의 이치같은 것이다.
하지만 이 C를 구하는 것은 신의 영역이다. 실제 내일의 날씨는 인간이 생각할 수 있는 범위 밖의 다양한 변수에 의해 결정된다. 인간은 결과에 영향을 미치는 다양한 변수 중에서 “그럴 듯한” 일부 변수만을 고려하여 일기예보를 작성한다. 따라서 위의 식을 다시
세우면, y = C(x, z)라고 할 수 있다. x는 Observable Variable, 즉, 관찰가능한 변수를, 그리고 z는 Unobservable
Variable, 즉, 관찰이 불가능한 변수를 의미한다.
다시 말해서, 인간의 능력으로는 완벽한 C를 구할 수 없다. 그러므로 기계학습에서는 C를 Approximation하여
Hypothesis라는 개념을 사용한다. Observable Variable x만을 고려하여
특정 Hypothesis h를 통해 예측을 수행하는 것이 기본 구조이다. 일반적으로 예측의 결과가 정답이 아니라 어디까지나 “예측”한 것임을 표현하기 위해 y에
Hat을 씌워서 표현한다.
이 Hypothesis는 관찰 가능한 수많은 x들을 학습 데이터로 활용하여 학습을 통해 도출할 수 있다. 특히 x와 y가 한 쌍으로 주어진다면, x가
주어질 경우 y가 발생한다는 것을 경험적으로 학습하게 되며, (x,
y) 쌍이 학습 데이터로 많이 주어질수록 경험이 축적되어 더욱 정확한 예측이 가능하게 될 것이다. 흔히
특정 결과를 결정짓는 요소와, 그 요소에 의해 도출된 결과가 함께 학습 데이터로 주어지는 경우를 지도
학습(Supervised Learning)이라고 한다. 학습을
통해 얻은 Hypothesis는 알려지지 않은 새로운 데이터의 Classification을
위해 종종 사용된다.
2. 확률모델의 기본개념
특정 현상을 발생시키는 요소에 대해 완벽하게 알 수 없다는 한계는 학습에 있어서 다양한 문제들을 야기한다. 예를 들어, 바람이 불었더니 사과가 떨어졌다는 관찰을 통해 “바람이 불면 사과가 떨어진다”라는
Hypothesis를 학습한다고 가정하자. 분명히 바람 외에도 사과를 떨어뜨리는 다양한
요소들이 존재할 것이다. 하지만, Observable Variable을
바람 하나만으로 설정했기 때문에, 만약 바람이 불었지만 사과가 떨어지지 않은 경우가 학습 데이터로 관찰된다면, 모순이 되어 학습이 불가능하게 된다.
이러한 문제는 확률모델을 도입하면 간단히 해결된다. 확률모델의 기본
아이디어는 “가장 확률이 높은 쪽을 선택하자”는 것이다. 예를 들어, 10번의 관찰 중 바람이 불었는데 사과가 떨어진 경우가 7번이라면, 바람이 불었을 때 사과가 떨어질 확률은 0.7이고, 떨어지지 않을 확률은
0.3이므로 “바람이 불면 사과가 떨어진다”라는
Hypothesis를 수용하는 것이다.
Classification 문제에서
k개의 Class C에 대한 분류를 진행한다고 하면, 확률모델에
기반한 Classifier는 다음과 같이 간단히 표현할 수 있다.
즉, 데이터 x가 주어졌을
때, 가장 발생 확률이 큰 Class로 분류하는 것이다. 이때 각각의 Class에 대한 확률은 베이즈 정리(Bayes’ Theorem)를 통해 간단히 구할 수 있다.
이 수식에 나타나는 각각의 확률들은 편의상 고유의 이름을 부여하여 부른다.
P(C|x): Posterior Probability
P(x|C): Class Likelihood
P(C): Prior Probability
P(x): Evidence
이 용어들을 사용해 베이즈 정리를 표현하면 다음과 같다.
따라서, 앞서 살펴본 Classifier의
분류 방법을 Maximum Posterior Probability Classification이라고 하기도
한다.
데이터 x가 주어졌을 때 두 가지 Class로
Classification을 한다고 가정하면,
이 두 가지 확률을 구한 뒤, 왼쪽이 크다면 C1으로 분류하고, 오른쪽이 크다면 C2로
분류하면 된다. Evidence의 경우 두 확률 모두 분모에 공통으로 가지고 있기 때문에 생략이 가능하다.
3. 예제
은행은 고객들에게 대출을 해줄 때의 리스크를 최소화하고 싶어 한다. 따라서 고객의 신용등급을 효율적으로 매기는 시스템이 필요하다. 만약 신용등급이 높은 고객에게 대출을 해주면 은행의 이익은 증대될 것이고, 신용등급이 낮은 고객에게 대출을 해주지 않는다면 손실(Loss)을 최소화할 수 있을 것이다. 그리고 신용등급이 낮은 고객에게 대출을 해줄 때의 손실은 신용등급이 높은 사람에게 대출을 해주지 않을 경우의 잠재적인 이득과는 독립적으로 생각을 해주어야 한다. 네 가지 경우를 모두 고려하여 은행의 손실을 최소화하는 것을 확률모델을 활용해 해결해보자.
우선 고객의 신용등급을 K개의 단계로 나누어 나타내는 Class C를 정의하고, a를 어떤 행위(action)라고 정의한다. 이 예제에서 ai는 어떤 고객의 데이터가 주어졌을 때 해당 고객이 Ci에 속한다고 결정을 내리는 것을 의미한다. 그리고 λik는 Ck에 속하는 고객에게 ai를 취했을 때 발생하는 손실이라고 정의한다. 즉, 실제로는 Ck에 속하는 고객을 Ci에 속한다고 판단하는 경우의 손실이다. 문제를 간단히 하기 위해 i=k인 경우 λik=0, 그리고 i≠k인 경우 λik=1이라고 가정한다.
그렇다면 어떤 고객의 데이터 x가 주어졌을 때, ai 행위를 취할 경우의 리스크(Expected Risk) R은 다음과 같이 모델링할 수 있다.
이를 바탕으로 은행의 신용등급 평가 시스템은 다음과 같이 간단하게 표현할 수 있다.
이는 곧 리스크가 최소가 되도록 고객을 Classification하는 문제이다.
예를 들어, 신용등급이 총 두 가지가 존재한다면 다음의 두 가지 리스크를 구하여 리스크가 적은 쪽으로 신용등급을 평가하면 된다.
이때 우변의 Posterior Probability들은 앞서 살펴본 베이즈 정리를 활용해 구하면 된다. 학습 데이터 x가 라벨과 함께 주어지는 Supervised Learning의 경우 P(C)와 P(x|C)의 실제 값은 간단히 구할 수 있다. 예를 들어, 전체 10명의 고객 중 C1에 속하는 고객이 6명, C2에 속하는 고객이 4명이라면 P(C1) = 0.6이고 P(C2) = 0.4이다. 마찬가지로 P(x|C)도 주어진 데이터를 바탕으로 단순히 카운트만 하면 구할 수 있다. 예를 들어, C1에 속한 6명의 고객 중 특정 조건을 만족하는 고객의 수를 n이라고 하면 P(x|C1) = n / 6이다. 조건부확률의 개념을 바탕으로 값들을 구하면 된다.
은행은 고객들에게 대출을 해줄 때의 리스크를 최소화하고 싶어 한다. 따라서 고객의 신용등급을 효율적으로 매기는 시스템이 필요하다. 만약 신용등급이 높은 고객에게 대출을 해주면 은행의 이익은 증대될 것이고, 신용등급이 낮은 고객에게 대출을 해주지 않는다면 손실(Loss)을 최소화할 수 있을 것이다. 그리고 신용등급이 낮은 고객에게 대출을 해줄 때의 손실은 신용등급이 높은 사람에게 대출을 해주지 않을 경우의 잠재적인 이득과는 독립적으로 생각을 해주어야 한다. 네 가지 경우를 모두 고려하여 은행의 손실을 최소화하는 것을 확률모델을 활용해 해결해보자.
우선 고객의 신용등급을 K개의 단계로 나누어 나타내는 Class C를 정의하고, a를 어떤 행위(action)라고 정의한다. 이 예제에서 ai는 어떤 고객의 데이터가 주어졌을 때 해당 고객이 Ci에 속한다고 결정을 내리는 것을 의미한다. 그리고 λik는 Ck에 속하는 고객에게 ai를 취했을 때 발생하는 손실이라고 정의한다. 즉, 실제로는 Ck에 속하는 고객을 Ci에 속한다고 판단하는 경우의 손실이다. 문제를 간단히 하기 위해 i=k인 경우 λik=0, 그리고 i≠k인 경우 λik=1이라고 가정한다.
그렇다면 어떤 고객의 데이터 x가 주어졌을 때, ai 행위를 취할 경우의 리스크(Expected Risk) R은 다음과 같이 모델링할 수 있다.
이를 바탕으로 은행의 신용등급 평가 시스템은 다음과 같이 간단하게 표현할 수 있다.
이는 곧 리스크가 최소가 되도록 고객을 Classification하는 문제이다.
예를 들어, 신용등급이 총 두 가지가 존재한다면 다음의 두 가지 리스크를 구하여 리스크가 적은 쪽으로 신용등급을 평가하면 된다.
이때 우변의 Posterior Probability들은 앞서 살펴본 베이즈 정리를 활용해 구하면 된다. 학습 데이터 x가 라벨과 함께 주어지는 Supervised Learning의 경우 P(C)와 P(x|C)의 실제 값은 간단히 구할 수 있다. 예를 들어, 전체 10명의 고객 중 C1에 속하는 고객이 6명, C2에 속하는 고객이 4명이라면 P(C1) = 0.6이고 P(C2) = 0.4이다. 마찬가지로 P(x|C)도 주어진 데이터를 바탕으로 단순히 카운트만 하면 구할 수 있다. 예를 들어, C1에 속한 6명의 고객 중 특정 조건을 만족하는 고객의 수를 n이라고 하면 P(x|C1) = n / 6이다. 조건부확률의 개념을 바탕으로 값들을 구하면 된다.
4. 확률모델의 이점
두 가지 Class로 Classification하는
경우에 각각의 Posterior Probability를 x에
대한 그래프로 나타내면 다음과 같은 양상이 나타난다.
특정 x에 대해 모든 Class들의
Posterior Probability를 합치면 1이 되고, 각 Class의 Posterior
Probability가 같아지는 교차점이 존재한다.
새로운 테스트 데이터 x가 주어졌을 때, 두 Posterior Probability의 교차점에 해당하는 k를 기준으로 두고, x < k인 경우 C1으로, 그리고 k < x인
경우 C2로 분류를 하면 된다. 이때 회색 음영 부분이 Error가 될 것이다. 이 Error
부분은 확률모델의 불가피한 오류에 해당한다. 예를 들어,
특정 테스트 데이터 x가 주어졌을 때 C2에
대한 Posterior Probability가 0.9이기
때문에 C2로 분류를 했다면, 0.1만큼의 확률로 정답이
아닐 수도 있다. 쉽게 말해서, 10번의 바람이 불었을 때
사과가 9번 정도 떨어졌다고 해서, 바람이 불 때마다 항상
사과가 떨어지는 것은 아닌 것이다. 10번 중 한 번은 사과가 떨어지지 않는다. 따라서 “바람이 불면 사과가 떨어진다”는 Hypothesis는 완벽하지 않다. 다만 해당 x에 대해 90%의
정확도와 10%의 Error를 가질 뿐이다.
이러한 오류는 확률모델의 특성상 피할 수 없기 때문에 확률모델의 타당성에 대해 의문을 제기할 수도 있지만, 사실 수학적으로 본다면 가장 바람직한 방법이다. 만약 위 그림의 k 지점 이외에 다른 지점을 기준으로 분류를 수행한다면, 회색으로 칠해진
Error의 영역이 더욱 넓어질 것이다. 따라서, 베이즈 정리를 기반으로 한 이 확률모델의 Classifier는 Minimum Error Classification, 즉, Error를
최소화한다는 결론에 이른다.
5. References
Alpaydın, Ethem. Introduction to machine
learning. Cambridge, MA: MIT Press, 2014. Print.







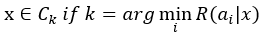



![[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIsNbQ5x9v-Z-WFogOWc-Lns6r9bJLAy9DBCVnl33dXsyXViNgjXrSvmnXzfOeL8m5Wb5VqImEKI0L-B9ZXzc2XmgWpmKCVFv87svXDsHG5WO_4sqVg-y2sRtuqbStxGf2HQ28wBdKIKBV/w72-h72-p-k-no-nu/%25EA%25B3%25A0%25EC%25A0%2595+%25EC%2586%258C%25EC%2588%2598%25EC%25A0%2590+%25EA%25B7%25B8%25EB%25A6%25BC.PNG)


![[R] 다중 회귀 분석 (Multiple Regression Analysis)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcv_-dAHO3EpXA84aAoidUMHJU6rKRsfYflGImKb829FBTDDyw01WftJ-PZD_UakTKM4u5KeubMIaau5zkwBtuYXPqdkpbvFOI_Tv3FFjKFYxkCaKknGFyclAUQrJlzyGwOtLzvotXhTFT/w72-h72-p-k-no-nu/%25ED%259A%258C%25EA%25B7%2580+%25EB%25B6%2584%25EC%2584%259D.PNG)

감사합니다. 학부 기계학습 강의에 어려움을 느끼고 있었는데 좋은 공부가 되었습니다.
답글삭제