자연계의 많은 현상들은 정규분포(Normal Distribution)을 따른다고 알려져 있다. 이렇게 데이터가 연속 확률 분포를 따를 경우에는 어떻게 학습을 하고, 또 이를 바탕으로 어떻게 분류를 해야 할까?
N(x: μ, σ2)에서의 Parameter는 μ와 σ이다. 기하학적으로 확률 밀도 함수의 위치는 μ가 결정하고, 폭은 σ가 결정하기 때문이다. 이를 바탕으로 NBC의 방법론을 활용하여 파라미터 학습(Parametric Learning)과 분류(Parametric Classification)를 진행하는 과정을 살펴보도록 하자.
2. Maximum Likelihood Estimation(MLE) Review
학습은 MLE를 통해 진행하는데, 구체적인 예시를 다루기 전에, 정규분포를 따르는 데이터에 대해 MLE로 어떻게 Parametric Learning을 하는지 간단히 살펴보도록 하자. MLE에 대한 자세한 설명은 관련 포스트를 참조하길 바란다.
(참고: https://arkainoh.blogspot.com/2017/10/parametric.learning.maximum.likelihood.estimation.html)
정규분포를 따르는 어떤 N개의 데이터 x의 집합 D가 주어졌다고 가정하자.
편의를 위해, 학습하고자 하는 Parameter를 θ라고 하면, MLE는 다음 식의 답을 구하는 과정이라고 할 수 있다.
수식을 쉽게 정리하기 위해, 시그마 부분을 L로 치환하자.
이 L을 미분으로 풀면, 평균과 분산을 쉽게 구할 수 있다. 이렇게 구한 평균을 Sample Mean이라고 하고, 분산을 Sample Variance라고 하자.
Sample Mean과 Sample Variance는 특정 데이터셋(Dataset), 즉, 특정 샘플(Sample)에 대한 학습 결과를 의미한다. 당연하게도 샘플의 데이터 수가 매우 크거나, 샘플 데이터의 분포가 전체 데이터의 분포와 유사할 경우, 학습 정확도가 크게 나타날 것이다.
3. Learning: NBC를 통한 학습
그렇다면, 앞서 살펴본 MLE를 바탕으로, 연속 확률 분포를 따르면서 여러 속성(e.g. 키, 몸무게, etc.)들을 가진 데이터, 즉, Multivariate Data에 대한 학습과 분류를 진행해보도록 하자.
NBC에 대한 배경지식이 필요하다면, 다음 링크를 먼저 학습하고 오는 것을 추천한다. 이 글에서 똑같은 예제를 사용한다.
(참고: https://arkainoh.blogspot.com/2018/07/nbc.html)
데이터 x는 다차원의 Vector로 주어지고, x가 어떤 클래스에 속하는지 나타내는 r이 One-hot Encoded Vector로 주어진다. r의 각 요소는 몇 번째 클래스인지를 의미한다.
예를 들어, 특정 사람의 키와 몸무게가 주어지고 남자인지 여자인지 구분하는 문제라고 생각해보자. 첫 번째 클래스가 남자, 두 번째 클래스가 여자라고 가정할 경우, 키가 180, 몸무게가 70인 남자의 데이터는 x = [180 70], r = [1 0] 이런 식으로 주어진다.
데이터가 가지는 속성의 인덱스 i는 Vector x의 i 번째 차원을 의미한다. 그리고 클래스 인덱스 k는 Vector r의 k 번째 차원을 의미한다. 위의 예시에서, x1 = 180, x2 = 70, r1 = 1, r2 = 0이다. 그리고, i <= 2, k <= 2가 성립한다.
이러한 정보들을 바탕으로 NBC를 통해 m(Sample Mean)과 s(Sample Variance)를 학습하는 과정을 의사 코드(Pseudo Code)로 나타내면 다음과 같다.
우선 위 코드는 구하고자 하는 값들을 초기화히고, 준비하는 단계이다. 실제 값을 구하여 반환하는 로직은 다음과 같다.
예시와 함께 살펴보도록 하자. 위의 예시처럼, 데이터 x는 키, 몸무게로 이루어진 벡터로 주어지고, 클래스는 남자 혹은 여자로 주어진다고 가정하자.
설명의 편의를 위해 One-hot Encoded Vector인 r대신 남, 여, ... 이런 식으로 클래스의 정보가 주어진다고 가정하겠다. 그렇다면, D를 구성하는 데이터들은 다음과 같이 주어질 것이다.
데이터들을 카운트하여 표에 정리했더니 다음과 같이 결과가 나타났다고 생각해보자.

전체 데이터 수 N = 10이기 때문에, Priority Probability는 P(C1) = 4 / 10 = 0.4이고, P(C2) = 6 / 10 = 0.6이다. 이전 글에서 데이터가 이산 확률 분포를 따른다는 가정 하에서는 데이터를 단순히 카운트하여 Class Likelihood를 P(xi = vj | Ck)라고 놓고 구할 수 있었지만, 이번에는 데이터가 연속 확률 분포를 따르기 때문에 불가능하므로, MLE를 통해 Parameter를 학습한 뒤에 Class Likelihood를 구하도록 한다.
예를 들어, m11과 s11은 다음과 같이 구할 수 있다.
m11 = (150 + 160 + 160 + 170) / 4 = 160
s11 = ((150 - 160)2 + 0 + 0 + (170 - 160)2) / 4 = 50
이와 같은 방식으로 m12, s12, m21, s21, m22, s22를 모두 구하면 학습은 완료된다.
4. Classification: NBC를 통한 분류
학습된 정보를 통해 분류를 할 때는, 각 클래스 중에 Posterior Probability가 가장 큰 클래스로 배정하면 된다. 앞서 Priority Probability와 Class Likelihood를 미리 구해두었기 때문에, Posterior Probability는 이 둘의 곱으로 간단히 나타낼 수 있다.
이 둘 중 값이 큰 쪽으로 Classification을 한다. 계산이 복잡하기 때문에 log를 취하여 구하도록 한다. 그리고 Vector의 차원(Dimension)을 고려하지 않고, 간단화해서 생각해보도록 하자.
위의 식을 x에 대한 방정식이라고 생각하고, σ, P(C1), P(C2)는 그 값이 미리 주어지는 상수라고 가정하자. 그렇다면 이 세 가지 상수의 값이 어떻게 주어지느냐에 따라 방정식의 그래프가 다양하게 그려지게 된다. 크게 세 가지 정도의 경우를 살펴보자.
(1) σ1 = σ2 & P(C1) = P(C2)
이 경우는 두 식을 간단히 정리하면 다음과 같다.
① (x - μ1)2
② (x - μ2)2
좀 더 직관적인 분석을 위해 그래프로 그려보면 다음과 같다. 회색으로 칠해진 부분은 Error 영역을 의미한다.
동일한 크기의 확률 밀도 함수가 나란히 나타나는 것을 관찰할 수 있다. 두 함수의 높낮이는 같기 때문에, 분류가 되는 기준은 정확히 x가 μ1과 μ2의 중간지점이 되는 경우이다. 즉, μ1과 μ2의 산술평균이 분류의 기준이 된다.
(2) σ1 = σ2 & P(C1) != P(C2)
앞선 경우와 달라진 점은 확률 밀도 함수의 높낮이에 변화가 있다는 점이다. 각각 곱해지는 상수의 값이 다르기 때문에 나타나는 현상이다. 이에 따라 분류의 기준은 μ1과 μ2의 산술평균과는 다른 지점으로 이동하게 된다. 결과적으로, 곱해지는 Prior Probability가 클수록 해당 클래스로 분류되는 면적이 증가한다. 이는 당연한 결과이다. Prior Probability는 전체 데이터에서 해당 클래스가 어느 정도의 비율을 차지하는지를 의미하므로, 이 값이 높을수록 해당 클래스로 분류될 확률도 증가하는 것이다.
(3) σ1 != σ2 & P(C1) != P(C2)
가장 일반적인 경우이다. 이 경우 σ 값이 상이하므로, 확률 밀도 함수들의 폭이 서로 달라지게 된다. 확률 밀도 함수의 폭과 높낮이가 모두 상이하기 때문에 수많은 경우가 있겠지만, 예시로 다음과 같은 그래프를 그릴 수 있다.
이 경우 단순히 특정 지점을 하나를 기준으로 C1 혹은 C2로 분류되는 것이 아니라, 두 확률 밀도 함수의 교차점들, 즉, 두 개의 지점을 고려해야 한다. 따라서 Decision Boundary가 두 확률 밀도 함수의 교점을 기준으로 C2, C1, C2로 나뉘는 형태로 나타난다.
5. 결론
데이터가 이산 확률 분포를 따를 때, 그리고 연속 확률 분포를 따를 때 각각의 경우는 NBC라는 큰 틀에서 큰 차이가 없다. 단, Class Likelihood를 구할 때 연속 확률 분포를 따르는 데이터셋의 경우에는 Parametric Learning을 통해 각 클래스별 확률 밀도 함수의 μ와 σ2를 구해야 한다는 점을 주의해야 한다. 결국 이 Parameter들에 의해 각 클래스의 확률 밀도 함수의 모양과 위치가 결정되고, 이를 바탕으로 Decision Boundary가 형성된다.
6. References
Alpaydın, Ethem. Introduction to machine learning. Cambridge, MA: MIT Press, 2014. Print.






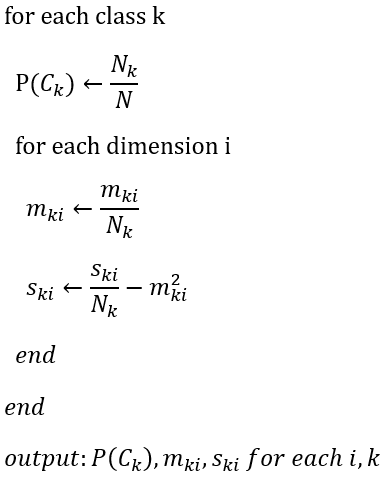








![[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIsNbQ5x9v-Z-WFogOWc-Lns6r9bJLAy9DBCVnl33dXsyXViNgjXrSvmnXzfOeL8m5Wb5VqImEKI0L-B9ZXzc2XmgWpmKCVFv87svXDsHG5WO_4sqVg-y2sRtuqbStxGf2HQ28wBdKIKBV/w72-h72-p-k-no-nu/%25EA%25B3%25A0%25EC%25A0%2595+%25EC%2586%258C%25EC%2588%2598%25EC%25A0%2590+%25EA%25B7%25B8%25EB%25A6%25BC.PNG)


![[R] 다중 회귀 분석 (Multiple Regression Analysis)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcv_-dAHO3EpXA84aAoidUMHJU6rKRsfYflGImKb829FBTDDyw01WftJ-PZD_UakTKM4u5KeubMIaau5zkwBtuYXPqdkpbvFOI_Tv3FFjKFYxkCaKknGFyclAUQrJlzyGwOtLzvotXhTFT/w72-h72-p-k-no-nu/%25ED%259A%258C%25EA%25B7%2580+%25EB%25B6%2584%25EC%2584%259D.PNG)

댓글 없음:
댓글 쓰기