마르코프 모델1: Observable Markov Model

1. 기본 개념
대부분의 데이터 분석 모델은 각각의 샘플 데이터의 발생 확률을 독립적이라고 보는 경우가 많다. 그러나 이는 인간의 언어나 주가 변동 등 연속된 데이터가 특정 패턴을 가진다는 사실을 반영하지 못한다. 예를 들어, 한 단어 안에서 알파벳 h는 x 다음에는 나타나지 않으며, t 혹은 s 다음에 나타날 확률이 높다. 즉, 단어 안에 나타나는 알파벳의 순서는 완전히 독립적이지 않다. 따라서 이와 같이 연속된 데이터가 서로 종속적이라는 관점이 필요하다. 이를 반영한 개념이 바로 마르코프 연쇄(Markov Chain)이다.
마르코프 연쇄는 이산적인 시간 흐름에 따른 시스템의 상태 변화를 확률적으로 나타낸 이산확률과정(또는 Discrete Markov Process)이다.
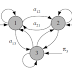
마르코프 연쇄는 FSM(Finite State Machine)처럼 특정 시점 t에 대한 State가 존재하며, 시간의 진행에 따라 특정 State에서 다른 State로 Transition을 한다. 각각의 State Transition의 확률은 시간의 영향을 받지 않는다. 예를 들어, State₁에서 State₂로 이동할 확률은 모든 시점 t에 대해 동일하다.
효과적인 설명을 위해 다음과 같은 Notation들을 정의한다.

S_i = i번째 State (1 <= i <= N)
q_t = 시점 t에서의 State (e.g. q₃ = S₆)
a_ij = S_i에서 S_j로 전이할 확률
pi_i = 첫 시점(t = 1)에서 S_i에 있을 확률, P(q₁ = S_i)

1차 마르코프 모델(First-order Markov model)에서는 특정 시점 t에서의 State는 바로 이전 시점 t-1에서의 State의 영향을 받는다고 가정한다. 이를 조건부 확률로 표현하면 다음과 같다.

P(q_t+1 = S_j | q_t = S_i, q_t-1 = S_k, ...) = P(q_t+1 = S_j | q_t = S_i)

이를 바탕으로 다음과 같은 관계가 성립한다.

a_ij = P(q_t+1 = S_j | q_t = S_i)

a_ij는 항상 0이거나 양수이며, N개의 모든 State로부터 S_i로 갈 확률을 더하면 1이 된다. 그리고, 첫 시점에서 모든 State에 있을 확률을 각각 더하면 합이 1이 된다.

2. Observable Markov Model
이 모델의 기본 전제는 매 시점마다 어떤 State에 있는지 관찰이 가능하다는 것이다. 즉, t가 주어지면 q_t를 알 수 있다. 따라서 시간 T 동안 어떤 순차적인 데이터가 관찰되었을 때, 이를 O(Observation Sequence)라고 하면 다음과 같이 표현할 수 있다.

O = {q₁, q₂, q₃, q₄, ..., q_T}

만약, 모든 a_ij 값들의 집합 {a_ij}와 pi_i 값들의 집합 {pi_i}가 주어진다면, 특정한 O가 발생할 확률을 쉽게 구할 수 있으며, 여러가지 O들을 트레이닝 데이터로 학습하여 a_ij와 pi_i 값들을 예측할 수 있다.
먼저, 특정 O가 발생할 확률은 다음과 같다.

P(O | {a_ij}, {pi_i}) = pi_q1 * a_q1q2 * a_q2q3 * ... * a_qT-1qT

예를 들어,

pi₁ = 0.4
a₁₁ = 0.1
a₁₃ = 0.2
a₃₂ = 0.5

이러한 정보가 주어졌다면, 특정 O(= {S₁, S₁, S₃, S₂})가 발생할 확률은 0.4 * 0.1 * 0.2 * 0.5가 된다.
반대로, K개의 O가 주어졌을 때, {a_ij}와 {pi_i}를 학습하는 것은 확률적인 추론을 통해 가능하다. 우선 pi_i는 K개의 O 중에서 q₁ = S_i인 O의 개수를 구하면 된다. 즉, q_i = (q₁ = S_i인 O의 개수) / K이다. 그리고 a_ij는 K개의 O 중에서 특정 시점 t에 대해 q_t = S_i인 모든 O들의 개수를 구하고, q_t = S_i와 동시에 q_t+1 = S_j를 만족하는 모든 O들의 개수를 구한 뒤에 나눗셈을 하면 된다. 즉, a_ij = (K개의 O 중 q_t = S_i와 q_t+1 = S_j를 만족하는 O의 수) / (K개의 O 중 q_t = S_i인 O의 수) 단, 모든 t에 대해 고려해줘야 한다.

3. 예시
Observable Markov Model은 항아리에서 공을 뽑는 것에 비유할 수 있다. 빨간색, 파란색, 초록색을 가진 세 개의 항아리가 있고, 한 항아리에는 같은 색의 공이 들어 있다고 가정해보자. 빨간색 공은 빨간색 항아리로부터만 뽑을 수 있으며, 파란색 공은 파란색 항아리로부터만 뽑을 수 있다. 뽑힌 공들의 색깔이 관찰 결과(O)이며, 각각의 항아리는 State를 의미한다. 즉, 어떤 색의 공을 뽑든지 해당 공이 어떤 항아리로부터 나왔는지 알 수 있기 때문에 Observable이라는 표현을 쓰는 것이다.

빨간 항아리를 S₁, 파란 항아리를 S₂, 초록 항아리를 S₃이라고 하고 각각 공을 5개, 2개, 3개 가지고 있다고 가정한다면, 첫 번째 차례에서 특정 색의 공을 뽑을 확률, 즉, pi_i 값들은 다음과 같다.

pi₁ = 0.5
pi₂ = 0.2
pi₃ = 0.3

또한, a₁₂는 빨간 항아리에서 공을 뽑고나서 다음 차례에는 파란 항아리에서 공을 뽑는 확률이라고 생각할 수 있다. 예를 들어, a₁₂ = 0.3, a₂₁ = 0.6이라고 하면 O = {빨간 공, 파란공, 빨간 공}, 즉, 첫 번째 차례에 빨간 공을 뽑고 나서 파란 공을 뽑고 다시 빨간 공을 뽑을 확률은 0.5 * 0.3 * 0.6이다.

4. Reference
Alpaydın, Ethem. Introduction to machine learning. Cambridge, MA: MIT Press, 2014. Print.