1. Introduction
최단 경로를 구하는 문제는, 다양한 알고리즘 중에서도 단연 핵심적이고 중요하다. 차량용 네비게이션에서 목적지까지 가장 빠르게 도달할 수 있는 경로를 찾거나, 모바일 로봇의 모션 계획을 수립하는 등 다양한 애플리케이션에 활용될 수 있다. 본 글에서는 유형 별로 최단 경로를 구하는 다양한 알고리즘에 대해 살펴보고, 해당 알고리즘의 정합성과 효율성에 대해 고찰해보도록 하겠다.
2. 최단 경로의 정의 (Definition of Shortest Path)
(1) Edge-weight function
Figure 2.1
예를 들어, Figure 2.1는 w(p) = -2인 경우이다.(2) Shortest Path
점 u에서 v에 이르는 최단 경로는 w(p)가 최소인 경로 p이다. 이때, u에서 v에 이르는 최단 경로의 Weight를 (2.2)와 같이 정의한다. 단, u에서 v에 이르는 경로가 없을 경우에는, δ(u, v) = ∞로 정의한다.
(3) Optimal Substructure
Theorem. 특정 최단 경로 내에 포함된 부분 경로(Subpath)는 반드시 최단 경로이다.
Proof.
Figure 2.2에서 v1에서 v6에 이르는 실선의 간선들이 최단 경로를 이룬다고 가정하자. 만약, 사각형 안의 v2에서 v5에 이르는 최단 경로가 점선의 간선일 경우, 즉, 실선의 간선들이 최단 경로를 이루지 않는 경우, v1에서 v6에 이르는 실선의 간선들이 최단 경로를 이룬다는 가정에 모순된다.
(4) Triangle Inequality
Theorem. 그래프에 속한 모든 점 u, v, x에 대해, (2.3)이 성립한다.
Proof. δ(u, v) > δ(u, x) + δ(x, v)라고 가정하자. u에서 x를 거쳐 v로 가는 최단 경로의 Weight는 δ(u, x) + δ(u, v)이다. 그런데, 이는 δ(u, v)보다 작다. 즉, u에서 v로 가는 최단 경로의 Weight가 δ(u, v)보다 작으므로 모순이다.
Figure 2.3
(5) Well-definedness of Shortest Paths
그래프에 포함된 특정 점 v에서 출발하여 v로 다시 돌아오는 경로 p가 존재하고, 이때 w(p) < 0인 경우를 Negative-weight Cycle이라고 정의한다. 만약, 그래프 내에 Negative-weight Cycle이 한 개 이상 존재한다면, 최단 경로가 존재하지 않을 수도 있다. Negative-weight Cycle을 순회할 때마다 w(p)가 무한히 감소하기 때문이다.
3. 최단 경로 구하기 문제의 유형 (Shortest Path Variants)
출발점과 도착점의 개수에 따라 최단 경로 구하기 문제의 유형이 나뉘게 되고, 유형 별로 상이한 알고리즘들이 사용된다. 총 네 가지의 유형이 있는데, 이는 다음과 같다.
(1) Single-source: 하나의 점 s가 주어졌을 때, s에서 나머지 모든 점에 이르는 최단 경로를 구하는 것이 중에서 Single-destination 문제는 Single-source 문제를 거꾸로 생각하면 같은 문제라고 할 수 있다. 또한 Single-pair 문제는 Single-source 문제의 일부에 해당한다. 따라서, Single-source와 All-pairs 문제를 중점적으로 다루도록 하겠다.
(2) Single-destination: 임의의 여러 점으로부터 하나의 점 v에 이르는 최단 경로를 구하는 것
(3) Single-pair: 한 쌍의 점을 각각 출발점과 도착점으로 하는 최단 경로를 구하는 것
(4) All-pairs: 그래프 내의 가능한 모든 쌍의 점들에 대해 최단 경로를 구하는 것
3-1. Single-source Shortest Paths
모든 점들의 집합 V에 속하는 한 점 s가 출발점으로 주어졌을 때, V에 속하는 모든 점 v에 대해 δ(s, v)를 구한다. 이때, 간선의 가중치는 양수일 수도 있고, 음수일 수도 있는데, 모든 간선의 가중치가 양수인 경우와 그렇지 않은 경우로 나누어서 살펴보도록 하자.
3-1-1. 모든 간선의 가중치가 양수인 경우
앞에서 언급했듯이, Negative-weight Cycle이 존재하지 않는다면 최단 경로는 반드시 존재한다. 따라서, 모든 간선의 가중치가 양수인 경우, 반드시 최단 경로를 구할 수 있다. 이때, 최단 경로를 구하는 방법에 대한 아이디어는 다음과 같이 Greedy Algorithm의 개념을 활용하는 것이다.
i. 출발점 s로부터 특정 점 v까지의 최단 경로를 안다고 가정할 때, v들의 집합을 S라고 한다.
ii. 매번 v ∈ V-S를 만족하면서 S에 인접한 점 v들 중에서, s에서 v에 이르는 경로가 가장 짧은 v를 채택하여 S에 포함시킨다.
iii. 채택된 v에 인접한 점들의 거리 정보를 갱신한다.
(1) Dijkstra's Algorithm
이 로직은 1956년에 Edsger Wybe Dijkstra가 고안한 알고리즘으로, Dijkstra's Algorithm이라고 불린다. s ∈ V를 만족하는 하나의 출발점 s에서 v ∈ V를 만족하는 모든 점 v에 이르는 각 최단 경로의 길이를 구한다. 이 알고리즘을 의사 코드(Pseudo Code)로 나타내면 다음과 같다.
d[s] ← 0이때, d[v] = δ(s, v)이고, Q는 V - S를 포함하는 우선순위 큐(Priority Queue)이며, Adj[u]는 점 u에 인접한 점들을 의미한다. 그리고 특정 점 u가 집합 S에 포함될 때 u에 인접한 점 v들의 d[v] 값들을 d[u] + w(u, v)와 비교하여 더 작은 값으로 갱신하게 되는데, 이 과정을 "간선 (u, v)를 Relax한다"고 표현한다.
for each v ∈ V - {s}
do d[v] ← ∞
S ← ∅
Q ← V
while Q ≠ ∅
do u ← EXTRACT_MIN(Q)
S ← S ∪ {u}
for each v ∈ Adj[u]
do if d[v] > d[u] + w(u, v)
then d[v] ← d[u] + w(u, v)
(2) 정합성 검증 (Correctness)
Lemma. d[s]를 0으로, d[v]를 ∞로 초기화하는 것은 그래프 내의 모든 점 v에 대해 d[v] ≥ δ(s, v)를 만족하게 만들고, d[v]의 값을 갱신하더라도 이 성질이 유지된다.
Proof. 만약 이것이 거짓이라고 가정해보자. 점 v가 d[v] < δ(s, v)가 되게 만드는 첫 번째 점이라고 가정하고, 점 u가 d[v]값을 d[u] + w(u, v)로 갱신하게 만드는 점이라고 가정하자. 이를 통해 유추하면, 점 u에 대해 d[u] ≥ δ(s, u)를 만족한다. 그런데, Triangle Inequality를 활용하여 생각해보면 다음과 같은 모순이 발생한다.
d[v] < δ(s, v)Lemma. s에서 v에 이르는 최단 경로 상에서 점 u가 v의 이전에 위치한다고 가정해보자. 그렇다면, 만약 d[u] = δ(s, u)이고 간선 (u, v)가 Relax되었을 경우, d[v] = δ(s, v)임을 만족한다.
≤ δ(s, u) + δ(u, v)
= δ(s, u) + w(u, v)
≤ d[u] + w(u, v)
Proof. 가정에 의하면, δ(s, v) = δ(s, u) + w(u, v)이다. 이때, d[v] > δ(s, v)라고 가정하면 d[v] > d[u] + w(u, v)가 성립한다. 왜냐하면 d[v] > δ(s, v) = δ(s, u) + w(u, v) = d[u] + w(u, v)이기 때문이다. 그러므로, 해당 Dijkstra's Algorithm은 d[v] = d[u] + w(u, v) = δ(s, v)로 d[v] 값을 갱신하게 된다.
Theorem. Dijkstra's Algorithm은 반드시 V에 속한 모든 점 v에 대해 d[v] = δ(s, v)인 상태로 종료된다.
Proof. 알고리즘이 진행되면서 집합 S에 v를 추가할 때마다 d[v] = δ(s, v)임을 보장하므로, 참임을 쉽게 알 수 있다.
Figure 3.1
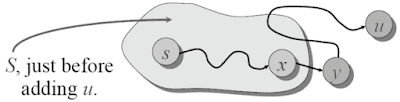
Figure 3.1처럼 만약 어떤 점 u가 d[u] > δ(s, u)인 상태로 집합 S에 추가된 첫 번째 점이라고 가정하고, 점 s에서 u에 이르는 최단 경로를 p라고 하자. 추가적으로, 점 y는 아직 집합 S에 포함되지 않은 점들 중에서 경로 p상에 위치한 첫 번째 점이고, 점 x는 경로 p상에서 y에 선행하는 점이라고 가정하자. 이때, 점 u가 d[u] = δ(s, u)를 위반하는 첫 번째 점이므로, d[x] = δ(s, x)이다. x가 집합 S에 포함될 때는 간선 (x, y)가 Relax되었을 것이고, 이는 d[y] = δ(s, y) ≤ δ(s, u) < d[u]임을 암시한다. 그러나, 처음에 집합 S에 점 y보다 u를 먼저 포함시켰다는 것은 d[u] ≤ d[y]임을 의미하므로 모순이다.(3) 시간 복잡도 (Time Complexity)
Time = Θ(V) ⋅ T(EXTRACT_MIN) + Θ(E) ⋅ T(DECREASE_KEY)
Dijkstra's Algorithm의 시간 복잡도는 우선순위 큐로부터 V개의 점을 하나씩 추출하는 과정과, E개의 각 간선을 Relax하는 과정을 수행할 때의 소요 시간을 합산한 것으로 요약할 수 있다.
Table 3.1
큐로부터 점 하나를 추출하는데 소요되는 시간을 T(EXTRACT_MIN)이라고 하고, Relaxation 과정에서 점의 d 값을 변경하고 큐 자료구조를 정비하는데 소요되는 시간을 T(DECREASE_KEY)라고 하자. 이 두 시간은 사용되는 자료구조의 종류에 따라 상이하다. Table 3.1은 자료구조별 시간복잡도를 빅 오 표기법(Big O Notation)으로 요약한 것이다.3-1-2. 간선에 가중치가 없는 경우
모든 간선에 가중치가 없는 경우는 (u, v) ∈ E인 모든 간선 (u, v)에 대하여 w(u, v) = 1인 경우와 동치이다. 즉, 모든 간선의 가중치가 동일하기 때문에 우선순위 큐를 사용할 필요가 없다.
(1) Breadth-first Search (BFS)
단순히 기본적인 선입선출(First in, first out, 줄여서 FIFO)의 큐를 사용한다. 초기화 과정은 이전의 알고리즘과 동일하지만, 출발점 s만 먼저 큐에 삽입한 뒤 시작하는 점에 차이가 있다. 매번 큐로부터 꺼낸 특정 점 u에 인접한 점들 중 d 값이 갱신되지 않은 점들을 찾아 d[u] + 1로 값을 변경하고 큐에 삽입한다. 최종 결과는 점 s에서 집합 V - {s}에 속한 모든 점들에 도달하기까지 거쳐야 하는 최소 간선의 개수, 즉, 최단 경로가 된다. 이 알고리즘을 의사 코드로 나타내면 다음과 같다.
d[s] ← 0(2) 정합성 검증 (Correctness)
for each v ∈ V - {s}
do d[v] ← ∞
ENQUEUE(Q, s)
while Q ≠ ∅
do u ← DEQUEUE(Q)
for each v ∈ Adj[u]
do if d[v] = ∞
then d[v] ← d[u] + 1
ENQUEUE(Q, v)
Idea. BFS에서의 선입선출 큐는 Dijkstra's Algorithm에 사용된 우선순위 큐의 동작을 모방한다.
Invariant. 선입선출 큐의 특성에 의해 점 v가 큐에서 점 u보다 먼저 추출되었다면, d[v] = d[u]이거나 d[v] = d[u] + 1임을 암시한다.
(3) 시간 복잡도 (Time Complexity)
Time = Θ(V + E)
선입선출 큐는 T(EXTRACT_MIN) = O(1), T(DECREASE_KEY) = O(1)이므로, 이를 반영하면 시간 복잡도는 Θ(V + E)이다.3-1-3. Negative-weight cycle이 존재할 수 있는 경우
만약 어떤 그래프 G = (V, E)가 Negative-weight Cycle을 포함한다면, 최단 경로를 구하지 못할 가능성이 있다는 것을 앞서 Well-definedness of Shortest Paths에서 살펴보았다. 이러한 경우, Negative-weight Cycle이 그래프 내에 존재하는지 탐지할 수 있는 알고리즘이 필요하다.
(1) Bellman-Ford Algorithm
Dijkstra's Algorithm과 마찬가지로, s ∈ V인 하나의 출발점에서 v ∈ V인 모든 점 v에 이르는 각 최단경로의 길이를 구한다. 그리고, 그래프 내의 Negative-weight Cycle의 존재유무를 판단한다. 이 알고리즘을 의사 코드로 나타내면 다음과 같다.
d[s] ← 0Bellman-Ford Algorithm은 Dijkstra's Algorithm과 달리 큐를 사용하지 않는다. Dijkstra's Algorithm에서는 큐로부터 추출한 특정 점에 인접한 간선들만 Relax를 했지만, Bellman-Ford Algorithm의 경우에는 모든 간선에 대해 Relax를 시도한다. Dijkstra's Algorithm은 Greedy Algorithm에 속하고, Bellman-Ford Algorithm은 Dynamic Programming에 속한다.
for each v ∈ V - {s}
do d[v] ← ∞
for i ← 1 to |V| - 1
do for each edge (u, v) ∈ E
do if d[v] > d[u] + w(u, v)
then d[v] ← d[u] + w(u, v)
for each edge (u, v) ∈ E
do if d[v] > d[u] + w(u, v)
then report that a negative-weight cycle exists
만약 |V| - 1회의 Iteration 후에도 d[v] 값들이 수렴하지 않는다면, 출발점 s에서 도달할 수 있는 Negative-weight Cycle이 그래프 내에 존재한다는 의미가 된다. 이를 통해 Negative-weight Cycle의 존재 여부를 탐지할 수 있다.
(2) 정합성 검증 (Correctness)
Theorem. 만약 그래프 G = (V, E)가 Negative-weight Cycle을 포함하지 않는 경우, Bellman-Ford Algorithm은 수행이 완료된 후 모든 점 v ∈ V에 대해 d[v] = δ(s, v)를 만족한다.
Proof. v ∈ V인 특정 점 v에 대해 출발 점 s에서 v에 이르는 최단 경로들 중에서 경로 상에 포함된 간선 수가 최소인 경로를 p라고 가정하자.
Figure 3.2
Figure 3.2에서 간선 (vi-1, vi)는, 총 |V| 번의 Iteration 중 적어도 i번째에서 Relax될 것임을 알 수 있다. 그리고 p가 최단 경로이기 때문에, δ(s, vi) = δ(s, vi-1) + w(vi-1, vi)를 만족한다.좀 더 상세히 설명하자면, 초기 상태에서는 d[v0] = 0 = δ(s, v0)이고, d[v] ≥ δ(s, v)를 만족해야 하기 때문에, 이어지는 Relaxation 과정에서 d[v0]는 변하지 않는다.
그런데, E에 속한 모든 간선에 대해 한 번씩 훑으며 Relaxation을 하는 것을 한 번의 Iteration이라고 했을 때, 첫 번째 Iteration에서 d[v1] = δ(s, v1)이 된다. 또, 두 번째 Iteration에서는 d[v2] = δ(s, v2)가 된다. 같은 방법으로, k 번째 Iteration에서는 d[vk] = δ(s, vk)가 된다.
그래프 G가 Negative-weight Cycle을 포함하지 않기 때문에 p는 단순 경로(Simple Path)가 된다. 가장 긴 단순 경로에 포함된 간선의 수는 |V| - 1보다 같거나 작다.
(3) 시간 복잡도 (Time Complexity)
Time = O(VE)
의사 코드에 의하면, 집합 E에 포함된 모든 간선을 Relax하는 과정을 |V| - 1회 반복하므로, 시간 복잡도는 O(VE)이다.
3-2. All-pairs Shortest Paths
모든 가능한 점의 쌍에 대해 최단 경로를 구하는 것은 Dijkstra's Algorithm을 |V|회 수행하면 된다. 이때, 시간 복잡도는 대략 O(VE + V2lgV)이다. 하지만, 그래프 내에 Negative-weight Cycle이 존재한다면 이 알고리즘을 사용하지 못할 것이다. 만약 그래프 내에 속한 모든 점에 대해 Bellman-Ford Algorithm을 사용한다면 시간 복잡도는 O(V2E)가 된다. 게다가, 그래프에 포함된 점의 개수가 n이라고 할 때, 간선의 개수가 n2 정도인 고밀도 그래프(Dense Graph)의 경우, 시간 복잡도는 Θ(n4)가 된다. 따라서 이러한 방법들 외에 어떤 효율적인 알고리즘들을 사용할 수 있는지 살펴보도록 하자.
(1) Definition of All-pairs Shortest Paths Problem
Input. 유향 그래프 G = (V, E)와 u ∈ V, v ∈ V일 때 G에 속한 모든 간선에 대한 Edge-weight Function w(u, v)가 주어진다. 이때, V = {1, 2, ..., n}이다.
Output. n x n 크기의 행렬을 결과로 도출해내며, i행 j열의 원소는 i, j ∈ V인 점 i에서 점 j에 이르는 최단경로의 길이 δ(i, j)를 나타낸다.
(2) Dynamic Programming
All-pairs Shortest Paths 문제는 Dynamic Programming의 관점에서 해결할 수 있다. n 개의 점을 포함한 유향 그래프를 나타내는 n x n 크기의 인접 행렬을 A = (aij)라고 정의하고, 점 i에서 출발하여 점 j에 도달할 때 최대 m 개의 간선을 사용하여 이루어지는 최단 경로의 가중치 값을 dij(m)이라고 정의하자.
그렇다면 Dynamic Programming을 위한 점화식은 (3.2)가 되며, 초기값은 (3.1)이 된다.
Proof. (3.2)의 최소값을 구하는 과정을 다음과 같이 의사 코드로 나타낼 수 있다.
for k ← 1 to n이는 앞서 언급된 최단 경로 구하기 알고리즘들과 동일하게, Relaxation 과정을 거친다고 할 수 있다. 즉, 출발점 i와 도착점 j 사이에 위치한 모든 점 k들(i와 j도 포함)을 조사하여, k를 거쳐가는 최단 경로들 중 가장 짧은 최단 경로를 채택하므로, 알고리즘의 결과인 δ(i, j)는 반드시 최단 경로의 길이를 나타낸다고 할 수 있다.
do if dij > dik + akj
then dij ← dik + akj
Figure 3.3
Note. 만약 그래프 내에 Negative-weight Cycle이 존재하지 않는 경우, δ(i, j) = dij(n - 1) = dij(n) = dij(n + 1) = ⋯을 만족한다. 단순 경로에 포함된 최대 간선의 수는 n - 1이기 때문에, 최단 경로에 포함될 수 있는 최대 간선의 수를 n - 1 이상으로 증가시켜도 dij(m)의 값은 변경되지 않을 것이다. 당연하게도, 경로 상에 Negative-weight Cycle이 존재할 경우, 경로 상에 포함되는 간선의 수를 증가시킬 때마다 dij(m)의 값은 점차적으로 감소하게 된다.(3) Matrix Multiplication Algorithm
n x n 크기의 행렬 A, B, C에 대해 C = A ⋅ B를 계산하는 과정은 (3.3)과 같다. 이 연산을 수행하기 위한 시간 복잡도는 기본적으로 Θ(n3)이다.
만약 (3.3)의 연산 중 "+"를 "min"으로, "⋅"를 "+"로 치환하면 (3.4)가 된다. 이는 (3.2)를 행렬의 곱셈 연산 문제로 바꾸는 초석이 된다.
임의의 점 i, j에 대해 dij(m) 값들의 집합을 행렬로 표현한 것을 D(m)라고 정의하고, (3.4)의 연산을 새로운 Matrix Multiplication "x"라고 정의하면, (3.1)과 (3.2)는 각각 (3.5)와 (3.6)으로 재정의할 수 있다.
"min"과 "+" 연산은 결합법칙이 성립한다. 따라서, 다음과 같은 성질을 관찰할 수 있다.
D(1) = D(0) ⋅ A = A1따라서, 결과적으로 D(n - 1) = (δ(i, j)) = An-1이 성립함을 알 수 있다. 이때, 행렬 곱셈 연산을 n 번하는 것과 마찬가지이므로, 시간 복잡도는 Θ(n ⋅ n3) = Θ(n4)이다. 이는 Bellman-Ford Algorithm을 n 개의 점에 대해 한 번씩 수행하는 것과 차이가 없다. 그러나, 기본적인 행렬 곱셈 연산이 아닌, 효율적인 행렬 곱셈 연산 알고리즘들을 적용한다면, 시간 복잡도를 대략 Θ(n3lgn) 정도로 줄일 수 있다.
D(2) = D(1) ⋅ A = A2
:
D(n - 1) = D(n - 2) ⋅ A = An-1
만약, Negative-weight Cycle의 존재 여부를 탐지하고자 한다면, 행렬 D(n - 1)의 대각선 원소들을 검사하여 음수 값이 존재하는지 판단하면 된다. 특정 점에서 출발하여 자기자신으로 다시 돌아오는데, 가중치가 음수라면, Negative-weight Cycle이 존재하는 것이기 때문이다. 이때, 행렬의 대각선을 검사하는데 O(n)의 시간이 추가적으로 소요된다.
(4) Floyd-Warshall Algorithm
Floyd-Warshall Algorithm은 Matrix Multiplication Algorithm과 같이 Dynamic Programming을 응용한 알고리즘이지만, 상대적으로 속도가 더욱 빠르고 구현이 쉽다. 특정 점 i에서 출발하여 점 j에 도달하고자 할 때, 중간에 거쳐가는 점은 집합 {1, 2, ..., k}에 속하는 점들로 제한한다. 이때의 최단 경로의 길이를 cij(k)라고 정의한다. 예를 들어, c15(3)은 점 1에서 출발하여 점 4는 거치지 않고 점 1, 2, 3 중 임의의 점들을 거쳐서 점 5에 도달하는 최단 경로의 길이를 의미한다. 따라서, cij(0) = aij이고 δ(i, j) = cij(n)이다.
cij(k) 값들을 구하기 위한 Dynamic Programming의 점화식은 (3.7)이다.
Figure 3.4
(3.7)을 그림으로 표현하면 Figure 3.4와 같다. k보다 인덱스가 작은 점들만을 거친 최단 경로와 점 k를 거친 최단 경로를 비교하여, 길이가 더 작은 최단 경로를 채택한다. 이를 의사 코드로 표현하면 다음과 같다.for k ← 1 to nIteration 과정에서 k가 증가하면서 cij(k)가 cij(k - 1) 값을 덮어씌우지만, cij(k)는 cij(k - 1)을 포함하는 개념이기 때문에 문제되지 않는다. 따라서, cij(k)를 3차원 행렬이 아니라, k를 고려하지 않은 2차원 행렬 (cij)로 구현하여도 문제없다.
do for i ← 1 to n
do for j ← 1 to n
do if cij > cik + ckj
then cij ← cik + ckj
의사 코드에 의하면 n 개의 점에 대해 3중 반복문을 통해 Iteration이 이루어지기 때문에 시간 복잡도는 Θ(n3)이다.
4. Conclusion
Table 4.1 Single-source Shortest Paths
최단 경로 문제는 유형에 따라, 그리고 그래프의 형태나 간선의 특징에 따라 다양한 알고리즘들이 사용된다. Table 4.1과 Table 4.2는 앞서 살펴본 알고리즘들의 대략적인 시간 복잡도를 요약한 것이다. 최단 경로 문제가 주어졌을 때, 문제의 유형을 잘 파악한 뒤 적절한 알고리즘을 선택하는 것이 관건이다.5. Source Code
https://github.com/arkainoh/algorithms/blob/master/c/GraphDijkstra.c
https://github.com/arkainoh/algorithms/blob/master/c/GridDijkstra.c
https://github.com/arkainoh/algorithms/blob/master/c/GraphBFS.c
https://github.com/arkainoh/algorithms/blob/master/c/GridBFS.c
https://github.com/arkainoh/algorithms/blob/master/c/BellmanFord.c
https://github.com/arkainoh/algorithms/blob/master/c/FloydWarshall.c
6. References
Introduction to Algorithms, 3ed, Cormen et al. and lecture notes of Demaine and Leiserson









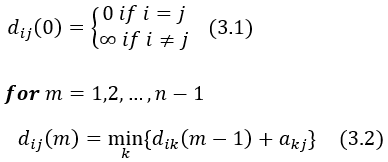




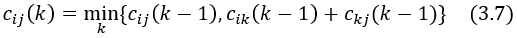



![[Algorithm] 최단 경로 구하기 (Shortest Paths)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiKXis_MkS9puWqfEqjSXc29vUjbNxQF9C25_MVNljtaVxwqw_80qr0bUb-nwEAsG9bZPJaeaPSguKcsvqGC8ncZV_52yNqlFsoe4LmjqOqVDlvZt0RXRPpxQ6NN0IqChWXGuOSR25J-36t/s72-c/header.png)
![[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIsNbQ5x9v-Z-WFogOWc-Lns6r9bJLAy9DBCVnl33dXsyXViNgjXrSvmnXzfOeL8m5Wb5VqImEKI0L-B9ZXzc2XmgWpmKCVFv87svXDsHG5WO_4sqVg-y2sRtuqbStxGf2HQ28wBdKIKBV/w72-h72-p-k-no-nu/%25EA%25B3%25A0%25EC%25A0%2595+%25EC%2586%258C%25EC%2588%2598%25EC%25A0%2590+%25EA%25B7%25B8%25EB%25A6%25BC.PNG)


![[R] 다중 회귀 분석 (Multiple Regression Analysis)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcv_-dAHO3EpXA84aAoidUMHJU6rKRsfYflGImKb829FBTDDyw01WftJ-PZD_UakTKM4u5KeubMIaau5zkwBtuYXPqdkpbvFOI_Tv3FFjKFYxkCaKknGFyclAUQrJlzyGwOtLzvotXhTFT/w72-h72-p-k-no-nu/%25ED%259A%258C%25EA%25B7%2580+%25EB%25B6%2584%25EC%2584%259D.PNG)

우와아아아아아 1도 모르겠다!!! 짱짱맨이었네요 블로그 짝짝
답글삭제