이 글에서는 일반적으로 널리 사용되는 부동 소수점(Floating Point)과 달리 다소 생소한 고정 소수점(Fixed Point)에 대해 알아본다. 일부 프로그래밍 언어의 경우 고정 소수점 방식을 기본적으로 제공해주기도 하지만, 많은 경우 실수 표현에 있어서 부동 소수점 방식을 기반으로 하기 때문에 고정 소수점 방식을 사용하고자 한다면 직접 구현하거나, 외부 라이브러리를 통해 사용해야 한다는 불편함이 있다. 이 글은 C++ 언어를 사용하여 고정 소수점을 직접 구현해보면서 깊은 이해를 하는 것을 목표로 한다.
우선 고정 소수점의 정의부터 간단히 정리한 후에 부동 소수점 방식의 수를 고정 소수점 방식으로 변환(Floating Point to Fixed Point Conversion)하는 법, 그리고 고정 소수점 방식에서의 사칙연산(Arithmetic Operations)에 대해서 코드와 함께 살펴보도록 하겠다. 이후 고정 소수점 방식을 사용하는 이유나 소수점의 위치를 설정하는 방법 등 심화적인 내용에 대해 다룰 것이다. 이 글에서 설명에 사용된 모든 코드는 깃허브(Github)에 업로드되어 있으므로, 전체적인 코드를 보고 싶다면 한 번 살펴보길 권한다.
2. 고정 소수점의 정의
고정 소수점은 쉽게 말해서 특정 숫자의 소수점의 위치를 말그대로 고정하는 방식을 뜻한다. 컴퓨터 언어에서의 데이터 타입은 항상 최대 길이가 고정되어 있기 때문에 이러한 아이디어가 생긴 것이라고 생각할 수 있다. 예를 들어, 32-bit 운영체제에서 int형의 크기는 32비트이므로 앞의 10개의 비트는 정수 부분을 표현하도록 하고, 나머지 22개의 비트는 소수점 이하의 부분을 표현하도록 할 수 있다. 소수점 위치를 어디로 설정해야 하는지에 대해서는 정해진 답이 없다. 사용자의 임의대로 설정하면 된다. 다만, 사용하는 수의 범위를 감안하여 오버플로우(Overflow)가 발생하지 않도록 설정해야 한다. 이와 관련된 내용은 뒤에서 더 자세히 다루도록 하겠다.
이 글에서는 연산의 효율성을 위해 이진법을 기반으로 하면서 부호가 있는 고정 소수점을 기준으로 한다. 음수를 표현할 때는 2의 보수(2's Complement)를 사용한다. 따라서 그림에서 볼 수 있듯이 가장 왼쪽의 1비트(MSB)는 부호를 표현하기 위한 비트(Sign)로 사용된다. 그리고 IWL(Integer Word Length)은 정수 부분을 표현하는 비트의 수를 의미하며, FWL(Fractional Word Length)은 소수점 이하 부분을 표현하는 비트의 수를 의미한다. 전체 비트의 수를 WL(Word Length)이라고 할 때, FWL = WL - 1 - IWL이 성립하므로, 고정 소수점을 정의하기 위한 Parameter는 WL과 IWL 두 가지만 있으면 된다. 즉, 전체 길이가 WL비트이면서 정수 부분에 IWL비트를 사용하는 고정 소수점의 경우 (WL, IWL)와 같은 투플(Tuple)로 간단히 정의할 수 있다. 이 글에서는 편의상 F(WL, IWL)로 표기한다. 위 그림의 경우 F(16, 3)에 해당한다.
3. 부동 소수점에서 고정 소수점으로의 변환
고정 소수점을 제대로 구현하려면 우선 부동 소수점의 기본 형식부터 자세히 살펴볼 필요가 있다. IEEE754의 표준을 따르는 32비트의 float 데이터 타입은 다음과 같은 정보를 담고 있다.
맨 왼쪽의 1비트는 부호(Sign)를 나타내는데 사용되며, 이어지는 8비트는 지수부(Exponent)를, 그리고 나머지 23비트는 실제 숫자들(Mantissa)을 표현하는데 사용된다. 이는 실수를 표현할 때 다음과 같이 정수 부분이 한 자리인 소수(가수)와 정수의 거듭제곱의 곱 형태로 나타낼 수 있다는 아이디어를 바탕으로 하는 것이다.
이 예시는 10진법을 기반으로 한 부동 소수점 방식으로 0.123을 표현한 것이다. 그런데, IEEE754의 float은 2진법을 기반으로 한다. 이는 (밑) 부분이 10이 아니라 2가 됨을 의미한다.
그렇다면, float의 세 가지 영역에 대해 자세히 살펴보도록 하자. 우선 맨 앞의 Sign 비트는 1일 경우 음수를 나타내고, 0일 경우 양수를 나타낸다. Exponent는 말그대로 (지수) 부분을 나타낸다. 단, 주의해야 할 점은 실제 (지수) 값에 127이라는 Bias를 더한 값을 저장하고 있다는 것이다. 예를 들어, 지수가 3인 경우 float의 Exponent 부분을 출력해보면 130이라는 값이 나온다. 따라서 실제 지수 값을 얻으려면 Exponent에서 127을 빼주면 된다. 마지막으로 Mantissa는 (가수) 부분을 나타낸다. 이진수의 경우 이 (가수) 부분에서의 정수 부분은 항상 1이 된다. 즉, 무조건 1.xxx와 같은 형태로 나타난다. 가장 왼쪽에 위치한 1을 기준으로 정수 부분이 한 자리수가 되도록 만들어주기 때문이다. 이러한 특성을 이용해 1비트를 절약하기 위하여 Mantissa에는 소수점 아래의 값들만 저장한다. 예를 들어, 1.11011이라는 수의 Mantissa는 맨 왼쪽의 1을 제외한 11011이 된다. 고정 소수점으로 변환할 때 이 점을 주의해야 한다.
이 정보를 바탕으로 고정 소수점으로 변환해주는 함수를 만들도록 하자. 그런데, 구현에 앞서 한 가지 짚고 넘어가야 할 것이 있다. 단순히 특정 위치에 있는 비트를 읽어서 처리를 하면 간단할 것 같지만, C++에서는 float으로 선언한 변수에 대해 비트 연산(Bitwise Operation)을 사용할 수 없다. 물론, 특정 위치의 비트에 접근조차 불가능하다. 하지만, 이는 기본으로 제공되는 ieee754.h 헤더파일을 통해 해결이 가능하다. ieee754.h에는 IEEE754 표준을 따르는 float의 Sign, Exponent, Mantissa 부분에 접근할 수 있도록 해주는 ieee754_float이라는 union이 정의되어 있다. 이를 통해 원하는 영역의 비트들을 int형으로 받아올 수 있다. (참고: https://stuff.mit.edu/afs/sipb/project/merakidev/include/ieee754.h)
앞서 고정 소수점의 정의 부분에서 언급했듯이, 이 글에서는 이진법을 기반으로 하면서 2의 보수법을 통해 부호를 표현하는 고정 소수점을 구현한다.
#include <stdio.h>fix 함수는 float형의 실수와 WL, IWL을 인자로 받아서 32bit의 int형 값을 반환한다. 유효한 비트들이 오른쪽으로 쏠려있기 때문에, 원하는 WL에 따라 작은 크기의 자료형(fix8, fix16 등)으로 형변환하여 사용하면 된다.
#include <ieee754.h>
#define SIGN 1
#define EXPONENT 8
#define MANTISSA 23
#define EXP_BIAS 127
#define INT_SIZE 32
typedef short fix16;
typedef char fix8;
int fix(float f, int wl, int iwl) {
ieee754_float standard;
standard.f = f;
int ret = standard.ieee.mantissa | (1 << MANTISSA);
int exp = standard.ieee.exponent - EXP_BIAS;
int fwl = wl - iwl - 1;
int fraction = MANTISSA - exp;
int filter = (1 << wl) - 1;
if(fraction > INT_SIZE) {
ret = ret >> fraction - INT_SIZE;
fraction = INT_SIZE;
}
ret = ret >> fraction - fwl;
if(standard.ieee.negative) {
ret = ~ret + 1;
}
return ret & filter;
}
float에서 fix로 변환을 하면서 중요한 점은, float이 2의 보수법을 사용하지 않는다는 점이다. 따라서 음수의 경우 2의 보수법을 적용해주기 위해 코드의 마지막 부분에 standard.ieee.negative를 확인하여 처리하는 것을 볼 수 있다.
이 함수를 통해 3.4567을 F(16, 3)와 F(8, 3)로 변환하면 약간의 오차가 있지만 유사한 값이 출력되는 것을 볼 수 있다. 정수 부분이 4자리인 이유는 맨 왼쪽의 비트가 부호를 표현하는데 사용되기 때문이다. F(16, 3)보다 F(8, 3)이 오차가 더 큰 것을 확인할 수 있다.
부호만 바꿔서 -3.4567을 고정 소수점 방식으로 변환하면 역시 유사한 값이 나오는 것을 확인할 수 있다. 한 가지 주의할 점은, 2의 보수법으로 음수를 표현할 때 정수 부분과 소수점 이하 부분을 따로 생각하지 않고 한 몸으로 생각한다는 것이다. 즉, 이 두 부분을 합쳐서 하나의 int형 값이라고 생각하고 2의 보수법을 적용하는 것이다. 따라서, 정수 부분의 이진수가 1100인 것을 보고 십진수로 표현하면 -4이기 때문에 틀렸다고 단정지으면 안된다. 결과로 나온 위의 두 이진수들을 더해서 0이 나오는 것을 확인하면 이러한 의문이 해결될 것이라고 생각한다.
4. 고정 소수점의 사칙연산
고정 소수점 방식의 꽃은 바로 사칙연산의 효율성이다. 앞선 예시를 통해 짐작했겠지만, 2의 보수법을 적용한 고정 소수점의 경우 int형의 값들과의 사칙연산 과정이 동일해진다. 복잡한 실수의 사칙연산이 단순한 정수의 사칙연산으로 간소화되는 것이다.
같은 IWL을 가진 고정 소수점끼리의 덧셈과 뺄셈은 정수의 덧셈과 뺄셈과 완전히 동일하다. 따라서 따로 추가적인 구현을 할 필요가 없다. 그러나, 곱셈과 나눗셈의 경우는 그렇지 않다. 곱셈과 나눗셈의 과정에서는 16비트 이상의 공간을 사용해야 값의 손실없이 정확한 결과를 얻을 수 있다. 정확히 말하자면, A * B 또는 A / B의 경우는 A와 B 각각의 전체 길이를 합한 만큼의 공간이 필요하다. 따라서, 이 글에서 구현한 fix16의 경우는 16 + 16 = 32비트 크기의 int형 변수를 여분의 공간(Extra Space)으로 활용하여 연산을 진행한다.
이진수의 곱셈과 나눗셈을 하나하나 뜯어보면 다소 복잡하지만, 결국 가장 중요한 것은 결과값의 소수점의 위치이다. 이것에 집중하면 간단하게 고정 소수점 사칙연산을 구현할 수 있다.
이 글에서는 같은 IWL을 가진 고정 소수점끼리의 사칙연산을 가정한다. 그렇다면 피연산자들의 FWL도 같게 되는데, 이를 L이라고 하자. 두 개의 고정 소수점 수 A와 B에 대한 사칙연산을 수행한다고 할 때, 결과값도 역시 FWL이 L인 고정 소수점 수가 나와야 한다. A와 B에서 소수점을 찍지 않은 상태의 정수 값을 각각 a와 b라고 하면 다음과 같이 고정 소수점 수를 분수로 표현할 수 있다.
구현의 특성상 고정 소수점 방식의 소수점은 실제로 찍는 것이 아니라, 가상의 점이기 때문에 이러한 표현은 유용하다. 예를 들어, 1.011이라는 이진수가 있다면 메모리에는 1011이라는 정수만 저장된다. 즉, 앞서 구현한 fix8 또는 fix16형 변수에 저장되는 실제 값은 정수인 a와 b인 것이다. 정수 부분의 길이가 1이라는 것은 사용자가 임의로 정하는 것(IWL)이기 때문에 별도로 표시되지 않는다. 따라서 1011과 같은 정수의 사칙연산으로 문제가 바뀌게 되는 것이다.
이 분수 표현을 바탕으로 사칙연산에 대한 각각의 식을 세워보자. 연산의 결과도 FWL이 L이어야 하므로, 분모는 항상 2의 L승으로 유지해야 한다는 것에 유념한다.
알다시피 덧셈과 뺄셈은 정수의 경우와 동일하게 진행하면 되지만, 곱셈과 나눗셈의 경우 추가적인 연산이 필요하다. 곱셈의 경우는 a와 b를 곱한 결과에 2^L을 나누어주면 되고, 나눗셈의 경우는 a에 2^L을 곱한 뒤 b로 나누어주면 된다.
2의 지수승을 곱하거나 나누는 행위는 시프트 연산(Bitwise Shift Operation)를 통해 간단히, 그리고 효율적으로 수행할 수 있기 때문에 곱셈과 나눗셈은 다음과 같이 구현하면 된다.
int mul_fix(int a, int b, int wl, int iwl) {
int c = a * b;
return c >> wl - 1 - iwl;
}
int div_fix(int a, int b, int wl, int iwl) {
int c = a << wl - 1 - iwl;
return c / b;
}
5. 고정 소수점의 장단점
고정 소수점의 장점은 크게 두 가지가 있다. 첫 번째는 연산 효율성이 높다는 것이다. 앞서 살펴봤듯이, 실수 사칙연산 문제가 정수 사칙연산 문제로 바뀌기 때문에 연산에 요구되는 시스템의 자원이 줄어들게 된다.
두 번째는 적은 수의 비트를 사용한다는 것이다. 이는 특히 최근 유행하는 뉴럴 네트워크(Neural Network) 기반의 딥 러닝(Deep Learning)에서 빛을 발한다. 딥 러닝에서는 무수히 많은 수의 float형 실수를 Parameter로 사용하기 때문에, 항상 메모리 문제에 시달리게 된다. 예를 들어, 특정 Layer의 Weight 행렬의 크기가 512 x 512라면, 행렬 연산을 위해 메모리 상에 32 x 512 x 512 = 8388608 = 1GB의 공간을 확보해야 한다. 만약 8비트의 고정 소수점 방식을 사용한다면, 이 크기를 4분의 1로 줄일 수 있다. 이러한 강점은 특히 임베디드 시스템처럼 하드웨어 자원이 한정된 환경에서 유용하다.
단점은 역시 수를 표현함에 있어서 정확도가 떨어진다는 것이다. float형에 비해 적은 범위의 수만 제한적으로 표현이 가능하기 때문에 정확도를 요구하는 문제에서는 적합하지 않다.
하지만, Qiu, Jiantao, et al. "Going Deeper with Embedded FPGA Platform for Convolutional Neural Network"에 의하면, CNN을 활용한 ImageNet 이미지 분류같은 복잡한 딥 러닝 문제에서 적은 비트 수의 고정 소수점을 사용하고도 정확도 손실이 그다지 크지 않다는 점이 인상적이다. 거의 절반 혹은 4분의 1의 Bandwidth만 사용하면서 정확도의 손실을 최소화할 수 있는 F(WL, IWL)을 사용하여 메모리 부담을 덜 수 있다.
6. 고정 소수점 위치 설정
고정 소수점의 위치는 사용자의 임의대로 Static하게 설정하는 것이지만, Overflow의 발생을 최소화하고 정확도를 최대한 높이기 위해서 Dynamic하게 자동으로 설정할 수도 있다. 이를 Dynamic-precision Data Quantization이라고도 한다. 이 방법은 사용할 실수들의 값을 미리 다 알고 있다는 가정 하에 이루어진다. 간단한 두 가지 방법을 살펴보자.
첫 번째 방법은 모든 수를 검토해서 정확도의 손실이 최소화되도록 고정 소수점 수로 변환하는 것이다.
사용하고자 하는 비트 수는 WL로 고정되어 있다고 가정하고, N개의 float형 실수 x가 주어졌을 때 IWL 값을 변경해보면서 정확도의 손실이 최소가 되는 IWL을 찾으면 된다. 단, 이 방법은 부동 소수점과 고정 소수점간의 연산을 별도로 구현해야 한다는 단점이 있다.
이를 보완하기 위한 두 번째 방법을 생각해보자. 고정 소수점의 위치를 설정할 때는 사용할 데이터의 정수 부분의 범위, 즉, IWL에 주목하면 된다. 정수를 Overflow 없이 모두 표현할 수 있는 IWL의 최솟값이 가장 이상적이다. IWL이 작을수록 FWL이 커져서 소수 부분을 더욱 정밀하게 표현할 수 있기 때문이다.
이렇게 각각의 실수 중 가장 정수 부분의 수가 큰 값을 구한 뒤 Log를 취하여 IWL로 설정하면 좀 더 효율적이고 직관적으로 최적의 고정 소수점 위치를 얻을 수 있다. 이를 간단하게 코드로 구현하면 다음과 같다.
#include <math.h>
int optiwl(float floats[], int len) {
int max, iwl = 0;
for(int i = 0; i < len; i++) {
int n = floats[i];
if(n < 0) n *= (-1);
if(max < n) max = n;
}
if(max) iwl = log2(max) + 1;
return iwl;
}
7. Source Code
https://github.com/arkainoh/fixedpoint
8. References
https://en.wikipedia.org/wiki/Fixed-point_arithmetic
http://bab2min.tistory.com/183
http://www.puntoflotante.net/FLOATING-POINT-FORMAT-IEEE-754.htm
Qiu, Jiantao, et al. "Going deeper with embedded fpga platform for convolutional neural network." Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. ACM, 2016.






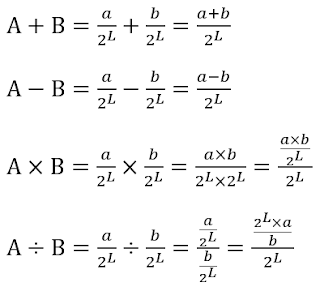



![[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIsNbQ5x9v-Z-WFogOWc-Lns6r9bJLAy9DBCVnl33dXsyXViNgjXrSvmnXzfOeL8m5Wb5VqImEKI0L-B9ZXzc2XmgWpmKCVFv87svXDsHG5WO_4sqVg-y2sRtuqbStxGf2HQ28wBdKIKBV/s72-c/%25EA%25B3%25A0%25EC%25A0%2595+%25EC%2586%258C%25EC%2588%2598%25EC%25A0%2590+%25EA%25B7%25B8%25EB%25A6%25BC.PNG)
![[C/C++] 고정 소수점의 모든 것 (All about Fixed Point)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIsNbQ5x9v-Z-WFogOWc-Lns6r9bJLAy9DBCVnl33dXsyXViNgjXrSvmnXzfOeL8m5Wb5VqImEKI0L-B9ZXzc2XmgWpmKCVFv87svXDsHG5WO_4sqVg-y2sRtuqbStxGf2HQ28wBdKIKBV/w72-h72-p-k-no-nu/%25EA%25B3%25A0%25EC%25A0%2595+%25EC%2586%258C%25EC%2588%2598%25EC%25A0%2590+%25EA%25B7%25B8%25EB%25A6%25BC.PNG)


![[R] 다중 회귀 분석 (Multiple Regression Analysis)](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcv_-dAHO3EpXA84aAoidUMHJU6rKRsfYflGImKb829FBTDDyw01WftJ-PZD_UakTKM4u5KeubMIaau5zkwBtuYXPqdkpbvFOI_Tv3FFjKFYxkCaKknGFyclAUQrJlzyGwOtLzvotXhTFT/w72-h72-p-k-no-nu/%25ED%259A%258C%25EA%25B7%2580+%25EB%25B6%2584%25EC%2584%259D.PNG)

df
답글삭제좋은 글 감사합니다.
답글삭제감사합니다 정말 도움 많이 되었어요ㅠㅠㅠ
답글삭제안녕하세요 혹시 ieee754.h가 Visual Studio 컴파일러에서는 제공을 안하는 건가요..
답글삭제덕분에 많이 배워갑니다. 감사합니다.
답글삭제